Have you heard the news? The world's tallest mountain got a little taller yesterday. At the start of the week, Mt. Everest's officially listed consensus height was 29,028.87 feet, but after Chinese and Nepalese authorities agreed on the results of a recent survey, it is now 29,031.7 feet.
Headlines around the world blared that Everest had just undergone a growth spurt. It hadn't—the only sudden change in Everest's height in the last decade, as we'll get into, was actually a negative one. But more to the point, the sudden confluence of the messiness of a seemingly simple question like "What is the shape of the Earth?", the inscrutability of geologic time, and scientifically illiterate headlines was more or less made for me. Before I took to writing for a living, I was on the honest path of an Earth scientist, and I graduated with a degree in geology.
A fellow student of mine in those days, Curtis Baden, is now in his seventh year of his PhD study at Stanford. During our time, we mapped a chunk of the Argentinean Andes, and though I split dramatically with my education, he is now on a lifer's path. The reception of the Everest news was inevitably overblown, and while well-actuallying it might be worth it, I think it's the perfect opportunity to get into the weeds on this stuff. What really is a mountain range? How special are the Himalayas? The geoid was in the news, for chrissakes.
The following interview has been lightly edited for clarity.
Defector: Mt. Everest did not become taller, obviously. But it is growing. However, there's also erosion, and the dynamics of the Indian Plate hitting the Eurasian Plate are not uniform. So, what's the deal, generally, with the Himalayas?
Curtis Baden: The short answer is: Yes, they're getting taller.
The Indian plate is still smashing into the Eurasian plate at a few inches a year in terms of horizontal velocity. A lot of that leads to uplift of the Himalayas, as the Indian plate is underthrust beneath the Eurasian Plate, and those mountains get taller. The funky thing is, just like you said, as that underthrusting happens, it's not just a continuous cycle. There are earthquakes, which cause a certain amount of motion, and [tension] also builds up between earthquakes, because it's still accruing even though the faults are "stuck." So interseismically, it might be being gradually pushed up in an elastic sense, like a rubber band.
During that big Nepal earthquake in 2015, Everest may have actually gotten shorter. It may have been elevated, and when the earthquake popped, it subsided a little bit.
Is that on the order of centimeters, inches, or feet?
It depends on the size of the earthquake. Per year, it's millimeters to centimeters in terms of build-up in between earthquake cycles. During an earthquake, it can be on the order of feet.
When you said that earthquakes can influence the height, I'm thinking, once-in-a-century events can push it an inch, which is like a decade of growth in a day, but that's amazing that it can be feet in a day.
I wouldn't say multiple feet, but it's on that order. Six to eighteen inches of change is not out of the question, and since there's so much collision happening in the uplift of Himalayas you get these odd fluctuations. It is hard to quantify.
That's aspect one, but two, it's hard to just get up there and measure. The guy who went up there to measure it with the Nepalese team lost a toe to frostbite, and this expedition mattered enough to him that he lost a toe. I hope it was a pinky toe and not one of the big ones.
There's so much traffic that ideally you could leave a constant receiver up there so it could see how the height changes over time. But it also depends on how you measure mountain elevation. If you've got a mountain, and you're measuring it above sea level, it depends on how you define "sea level." Do you remember talking about the geoid estimate in undergrad?
Yeah, I remember one of the first amazing things I learned was this idea that basic aspects of the Earth like "sea level" and "the shape of the Earth" were always in contention and kind of fundamentally impossible to have a unified measurement of, since it's essentially a series of averages that are always changing and equilibrating. The idea that it will ever have an absolute elevation seems impossible.
To your point, one metric that you might take for measuring mountain height would be furthest from the Earth's core. Because of the obliquity of the sphere, the tallest mountain on Earth by that metric is actually this 20,000-foot peak in Ecuador [Note: Mt. Chimborazo] just because the Earth is more bulbous at the equator. Everest isn't even in contention. The fact that this mountain that is 9,000 feet shorter than Everest is amazing.
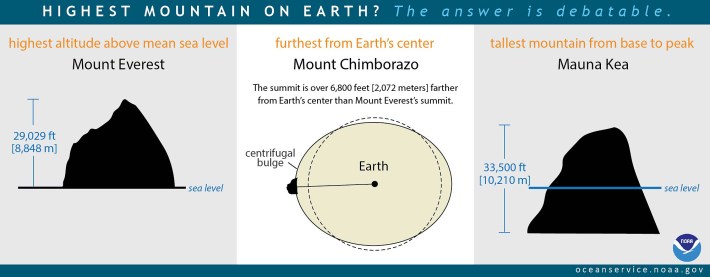
That's amazing, and it reminds me of Mauna Kea that's technically the tallest mountain on Earth. But the way we think about mountains is that they're all like the Lonely Mountain from Lord of the Rings, a perfect snowcapped triangle. Anyone with a faint understanding of geology understands why that's not the case, but in the case of the Himalayas, it might be worth understanding how different geologic time is. We can conceive of India as something that hit Eurasia, and then stopped. Whereas from the God view, that's actively happening still.
Totally, and it's super recent too. The Himalayan collision started 50 million years ago. That's nothing, the Sierra Nevada are older than that.
There's this mystery of how old the Sierras are. I didn't necessarily realize that they're being uplifted fairly—not "rapidly"—but the question of how old they are, that's active, right?
Interestingly, another PhD student that recently graduated, one of their projects was associated with dating the cooling of those magmas.
The granites?
The granites, yeah. And the answer depends on how you define "age." The rocks in the Sierras are on the order of 100 million years old. There's still active mountain building at that time, since you have these fairly buoyant bodies of rock put into the crust and the crust rises a little bit. But even after that happens, and the basin and range province starts to develop and normal faults start to develop and those high eastern Sierra escarpments like Mt. Whitney form, is the age of that specific section really the answer to "how old" they are? What really is a mountain range age?
That's a good question, and this is another element of the idea that geologic time is fundamentally incompatible with our understanding of mountains as static. Also, these answers are different across geologic space. This is not only happening along the length of the Sierras, but between depths as well. Is the batholith still down there? Is subduction still actively happening?
Not where we are, because there's the trade-off of the subduction of the Juan de Fuca plate.
Oh, right, the triple junction. Could you explain that to the reader?
There's a location off the coast of northern California called a triple junction. That's essentially where the San Andreas Fault—which is a strike-slip fault where the plates move horizontally relative to one another—meets up with a separate type of plate boundary where the Juan de Fuca plate starts to subduct under the North American plate. There are some super cool animations that Tanya Atwater made.
This animation from Dr. Tanya Atwater shows the plate tectonic history of the northeast Pacific and western North America, 38 million years ago to Present (stable North America held fixed). https://t.co/S6kjlWTi8g #platetectonics #geology pic.twitter.com/U6U0p4APcN
— IRIS Earthquake Sci (@IRIS_EPO) May 29, 2018
North of that, all the way up to Seattle and beyond, that's the subduction boundary. If you've heard about the massive seismic hazard that threatens Seattle as we speak, that's because there's active subduction going on, which produces the Cascade volcanos.
I've thought about this a lot: if you start in Southern California and zip your way up the Pacific Crest Trail, you can see, roughly, the history of subduction and what has followed along the Pacific Margin. You have these super-old, gross, eroded granites that just fall apart in your hand, to these massive Sierran peaks, to old active volcanos like Shasta, and then you go up to these really tall active mountains like Rainier and Mount St. Helens. It's so fascinating to me.
Thinking further about North American mountains, I remember learning and uncritically accepting that the Appalachians were once the premier mountain range in the world and were once taller than the Himalayas. Is that right?
I've heard that as well. Somebody's probably dedicated their academic career to studying this, so I wouldn't be the authority here, but to my understanding that's right. They essentially infer that from the complex sets of metamorphic rocks and structures that they see today. And they look at how deep those rocks must have been to form the way they did an they extrapolate upwards from that and say, "Okay well if these are here now, and they must have been this deep, this is what this mountain range might have looked like to form some of these rocks."
The idea that this extinct mountain range that could have been as tall as the Himalayas is just sitting at a super-low elevation along the Eastern seaboard is mind-blowing to me.
That history plus the present-day Himalayas really just shows you that it's uplift vs, erosion, and once uplift stops, erosion wins, right?
Totally. I'm working on a paper currently that's an attempt to bridge timescales we observe over a human lifetime to millions of years of geologic deformation. How do you get from an earthquake to the deformation you observe over millions of years? Because you're branching from seconds during an earthquake to millions of years, and then from millimeters of motion to tens and hundreds of kilometers of displacement across something like the San Andreas Fault.
How do you bridge these elastic cycles of earthquake jolts with the long-term, permanent deformation that you observe in the crust? Speaking to your point, the dimensions of a mountain range are governed by a combination of this seismic activity with, yes, erosion and also isostasy. [Note: Isostasy refers to the dynamic balancing of the Earth's solid crust on top of the relatively liquid-like mantle.]
If you develop this massive mountain range, it's pretty heavy. Earth's mantle is not solid, at least over geologic time scales, and so it sags. As it sags, that lowers the mountains too, there are so many complex factors that go into the development of a mountain range over time. From a nerdy perspective, it's exciting.
It's also kind of beautiful. At any given point in natural history, it doesn't matter where you are along the line: not only the physical forms of the Earth, but the whole arrangement of the world will look different. In a thousand years, it will look slightly different, in a million, it might look very different. Something will happen! I think that's kind of amazing, and it centers once again that the Earth is a very dynamic thing even if we don't necessarily see it that way.
Speaking of isostasy, something I thought was really cool was that the Great Lakes region and a lot of Canada is "bouncing back" because there was this big ice sheet pushing the world down. And now it's rising back up like a cake being baked.
You don't really think about how much these kilometers-thick ice sheets might weigh, but for anyone who's lived in a snowy climate, you know how heavy a foot of snow can be. Think about kilometers worth, yeah that's going to weigh a whole of a lot.
[Note: At this point, Curtis and I went on an extremely long digression about the ocean, which is a hostile, unexplored, and unmapped alien landscape covering two-thirds of the planet.]
You know about Olympus Mons on Mars, right?
Maybe you can tell me if I'm wrong, but I have a theory. If you look at Olympus Mons, it's not prominent. There's no spikiness to it.
Olympus Mons on Mars is largest #volcano in our solar system. Nearly 400 miles wide and rises 16 miles https://t.co/3MSo7w50gQ #MagmaMonday pic.twitter.com/54he4Jvuwj
— USGS (@USGS) February 13, 2017
Right, it's not at all spiky like some of our mountains.
Is that because there are fewer erosive forces on Mars?
Kind of. So on Mars, they don't have plate tectonics like we do here on Earth. If you have a magma source thats just constantly feeding a volcano without the overriding plate moving at all, the thing just erupts and then spills and erupts and then spills. There's nothing to move it such that it's going to produe magma in a different place.
Take the Hawaiian island chain for example: Instead of moving the hotspot and generating all these distinct islands, if you fixed it to a point, and erupted all of that lava in one prominent volcano, it's going to get huge. Repeat that for millions of years in solar system time, and yeah, of course you're going to make a massive volcano. To your point, we're starting to discover what the water cycle on Mars looked like at some point. To my knowledge, we don't have the massive amounts of erosive forces or bioturbation, because life plays an important role, or glaciers. There aren't these massive forces that take high rocks and distribute them to areas of lower elevation. I think that's why we see what we do.
That's fascinating. Because Mars is fairly Earthlike, generally.
Sure.
And if you change the fundamental aspect of the composition of the planet's core and what that magma distribution looks like, you change everything about the topography of the planet.
Yeah, and the more I study earth sciences, the more of an awesome thing plate tectonics turns out to be. The types of rocks you generate are amazing. Would we see some of these deeply buried metamorphic rocks at the surface if we didn't have a process to get them there in the first place? As these plates move around and smush each other, it brings that deep material up to the surface and we get to see them. Like the Sierra granites, those are volcanic roots we'd never see. They're usually tens of kilometers below the surface, and we're only seeing them because of these active forces associated with plate tectonics.
I guess, to wrap up here, do you have any interesting little topographic trivia the readers should know? Mine is always that there are glaciers in Indonesia and New Guinea, though not for long.
Here's one, and it directly relates to Everest. The rock atop Everest is actually a limestone, which means it was formed in a shallow sea. So the rock at the top of the world was actually underwater 50 million years ago. In geologic time, that's a snap. If you were to dig, under the snow, there are actually preserved fossils in the unit that composes the tallest mountain on Earth.
You can observe the Earth on any time scale you choose, so long as you have a way to measure it. The earthquake and earthquake-cycle measurements, you see how the Earth behaves in minutes to decades. A river that erodes captures timescales on the order of tens of thousands of years. The topography shows hundreds of thousands of years. In the past few years, there's been an explosion of geochemical data in terms of thermochronology that shows how erosion and exhumation brings rocks to the surface, and that captures a cycle over millions of years. And then you look at the fact that this limestone is on top of the world, 30,000 feet above the ocean, that captures it at a different scale .You really do have to look at it at every single set of observations over a vast set of time scales to understand how the Earth works dynamically. You can't just take any one snapshot and say, "That's how it works."






